Matemáticas, metodología manipulativa vs metodología tradicional

Este artículo pretende ser una investigación-acción sobre las medidas de masa. Habiendo encontrado el problema de que a los alumnos les resulta difícil de comprender estos contenidos sobre capacidad que se presentan en un libro de texto de forma teórica, la solución que propongo es enseñar estos contenidos de forma manipulativa para que así sean más significativos para los alumnos. Para comprobar la efectividad de la acción, se van a comparar dos grupos, uno de ellos seguirá la metodología tradicional y el otro será con el que se lleve a cabo la acción propuesta.

Palabras clave

Matemáticas, metodología manipulativa, medida, capacidad, masa.

This article is a research-action about measures of capacity and mass. Having found the problem that students have difficulties to understand these contents presented in a textbook, the solution I propose is to teach these contents in a manipulative way, so that, they are more meaningful for students. To test the effectiveness of the action, two groups are compared, one of them will follow the traditional methodology and the other will follow the proposed action.

Keywords

maths, handling methodology, measure, mass, capacity

1. Introducción

Actualmente, en las aulas de primaria, nos encontramos con el problema de que la mayoría de los alumnos no son capaces de resolver los problemas matemáticos de una forma razonada, sino que se basan en buscar el tipo de cuenta que tienen que hacer para dar una solución, llegando al punto de la intervención del azar en este caso. Aunque por todos es bien sabido que, para poder conseguir un aprendizaje significativo es fundamental el razonamiento lógico, no se le da la importancia que se le debería dar.

En el caso de la medida, nos encontramos con un doble problema. El primero, y más genérico, es que, al estar hablando del área de matemáticas, ya supone un bloqueo para la mayoría de las personas que se enfrentan a esta área. A este problema se suma el segundo, lo abstracto que resulta el tema de la medida con relación a la cantidad de tiempo que se le dedica a este tema dentro de las aulas. Dejando, así, completamente de lado el aprendizaje significativo.

El objetivo de esta investigación es proponer una renovación en la enseñanza de las matemáticas pasando del libro de texto a materiales manipulativos. Con este trabajo se pretende llevar a cabo una investigación acción referente a la forma de trabajar la medida dentro de las aulas.

2. Revisión teórica sobre la medida

2.1. Las matemáticas en la vida real

Las matemáticas son útiles en el momento en que pueden ser aplicadas a la resolución de problemas (Cockcroft, 1985 c.p. Fernández, 2006), pero el problema principal que nos encontramos es que dentro del aula realizamos problemas de una forma que luego no nos son útiles en reales en la vida real (Fernández, 2006).

Este hecho hace que la sociedad de hoy en día no vea útiles las matemáticas, es más, son vistas como algo inaccesible, algo para lo que se necesitan unos conocimientos muy complejos, lo cual llega a convertir esta área en un importante filtro selectivo del sistema educativo. La sociedad no es consciente de que las matemáticas son parte del día a día, incluso las utilizamos de forma efectiva cuando no somos conscientes de que estamos resolviendo problemas. Blanco y Blanco (2009) plantean que el uso de las matemáticas en la vida cotidiana está contrapuesto al uso en el aula, ya que la gente se bloquea por el hecho de pensar que está usando las matemáticas, aunque son capaces de utilizarlas de forma satisfactoria si no sabe que las está utilizando.

De forma que en el momento en el que la mayoría de la sociedad es consciente de que tiene un problema matemático ante sus ojos, surgen los bloqueos y las inseguridades puesto que en el colegio no han sabido encontrarles la utilidad y/o han fracasado en esta área. Según Blanco y Blanco (2009) es necesario acercar las matemáticas al contexto real puesto que los problemas que se plantean en el aula exigen a los alumnos a utilizar estrategias que luego no utilizaran en la vida cotidiana. Los alumnos se acostumbran a buscar un algoritmo, que se han aprendido de memoria, para resolver el problema, suelen recurrir al libro para ver qué están aprendiendo en ese momento y así utilizan el algoritmo que toca. Es una forma de aprenderse las matemáticas de manera memorística y no razonando.

Es por todo ello, que es necesario plantearse una serie de estrategias para poder ayudar a los niños desde pequeños en la resolución de problemas. Existen varias fases y subfases para la realización de un problema (Polya, 1992 c.p. Fernández, 2006): comprender el problema, concebir un plan y visión retrospectiva. A partir de aquí se puede empezar a formular estrategias para conseguir el éxito en la resolución de problemas.

2.2. El problema de la medida

Como ya se ha visto, varios autores citados anteriormente dicen que, las matemáticas son útiles cuando las podemos usar en la vida real, que es donde surgen problemas que se deben saber resolver. Pero ¿qué pasa con la medida? Queda constancia de que entran dentro de los contenidos que se deben estudiar en la Educación Primaria, pero suponen un problema general en su enseñanza, puesto que en la escuela se abandona la parte de medición efectiva de objetivos porque presuponen que el alumno lo aprenderá en su vida personal y familiar. Por lo que la escuela convierte en objetos didácticamente invisibles saberes y conocimientos que, más adelante, el alumno necesitará para adquirir nuevos conocimientos o para su vida personal. (Chamorro, M, 2005).

Chamorro (2005) hace referencia a que el contenido de la medida resulta difícil tanto para alumnos como para maestros, los cuales se limitan a enseñar el trabajo formal de cambio de unidades del Sistema Métrico Decimal, el cual es presentado de forma algorítmica y se practica con los problemas que plantean los libros de texto. Por su parte, los alumnos, encuentran grandes dificultades para darle un sentido a estos contenidos, puesto que son aprendidos de forma mecánica y memorística, nunca fuera de la escuela o de los libros de texto. Siendo así, es normal que los profesores digan que son contenidos muy abstractos y complicados de enseñar de forma significativa. Para conseguir acercar este tipo de contenidos a los niños es necesario saber cómo se forma el aprendizaje de la medida en nuestros alumnos.

Además, es importante tener en cuenta que existen diferentes tipos de situaciones a las que ellos deben enfrentarse. Es necesario dejar el papel y lápiz a un lado y pasar a la acción, puesto que solo se puede aprender a medir midiendo y discutiendo las estrategias utilizadas. Vamos a ver el tipo de actividades que se deberían trabajar (Godino, 2002):

1. Actividades de percepción y comparación: estas actividades deben apoyarse en la intuición de los alumnos y en sus experiencias informales, así les será más sencillo comprender los atributos que se miden y el significado de medir. Los alumnos deben explorar como cambian algunas medidas de los objetos tras someterlos a ciertas trasformaciones.
   • Se pueden realizar actividades como comparar el peso de objetos entre sí. Se les puede pedir que los ordenen por orden según ellos experimenten al manipularlos.
2. Actividades de estimación: consiste en realizar juicios subjetivos sobre la medida de los objetos. La estimación es muy útil en las actividades que realizamos en la vida diaria, por lo que se debe desarrollar esta destreza en la escuela. Además, las actividades de estimación de medidas ayudan a los alumnos a entender los distintos aspectos que se ponen en juego. El problema, según Castro (2001), es que este tipo de actividades se trabaja muy poco en las aulas por razones como: los profesores no se sienten competentes para enseñar esto puesto que los adultos no solemos tener desarrollada esta habilidad; no disponen de orientaciones de cómo realizar este tipo de actividades o no se tiene en cuenta el tiempo necesario para desarrollarlas.
   • Se puede solicitar a los alumnos que estimen pesos o cantidades con o sin la unidad presente, pero sin utilizarla. También es necesario realizar bastantes actividades de este tipo, puesto que con el ensayo error se irán mejorando las estimaciones y mediciones.
3. Actividades de medición: hacer mediciones es realmente importante. «Medición sin acción es meramente un tipo de rutina memorística o ejercicio intelectual» (Godino, 2002: 646). Queremos que los niños, además de memorizar el Sistema Métrico Decimal, tengan experiencias en todas las áreas de la medición y sean capaces de medir precisa y consistentemente. Las actividades de estimación de medidas permiten que los alumnos se centren en los atributos que miden, el proceso que siguen y el tamaño de las unidades. Por lo que así, los alumnos se darán cuenta de que con frecuencia es suficiente con dar una estimación de lo que mide el objeto y que no es necesario usar instrumentos de medida en todas las circunstancias.
   • Se puede facilitar al niño balanzas y/o vasos graduados para que ellos mismos comprueben las características de los objetos medidos.

3. Caso práctico

3.1. Identificación del problema

En general, el problema consiste en que los alumnos no relacionan la teoría que aprenden sobre el Sistema Métrico Decimal con la práctica en la vida real, por lo que a la hora de utilizarlo en situaciones cotidianas para resolver los problemas que se les puede plantear respecto a la medida, no son capaces de crear puentes entre el conocimiento que tienen sobre el tema y el problema que se les presenta.

3.2. Formulación de hipótesis

Si se consideran las notas de los alumnos como una variable dependiente del tipo de instrucción que se imparta (variable independiente), se puede decir que la variable dependiente será superior dependiendo del tipo de variable independiente que se utilice. Si se hace que los alumnos utilicen instrumentos de medida y los usen en actividades manipulativas (teniendo en cuenta los estadios por los que pasa el alumno, los pasos que siguen para constituir la unidad y las situaciones que deben experimentar), se logrará que sean capaces de dar un significado a la unidad de medida que están utilizando, por lo que los alumnos serán capaces de utilizar la medida con mayor eficacia en las situaciones de la vida real. Esto se traduce en que los resultados obtenidos siguiendo una metodología manipulativa serán superiores a los obtenidos siguiendo una metodología más tradicional.

3.3. Explicación de la selección de muestra

Para comprobar estas hipótesis se va a comparar los resultados de dos grupos. Estos grupos son dos clases de 4º de Educación Primaria del mismo colegio, por lo que son niños con edades comprendidas entre los 9-11 años. Los dos grupos están muy igualados en cuanto a los resultados académicos que les preceden, por lo que se puede decir que no existen ventajas respecto de un grupo al otro.

A los dos grupos se les va a pasar la misma prueba inicial antes de empezar a trabajar el tema. Ambos grupos verán los mismos contenidos, pero de diferente forma: Uno de los grupos (a partir de ahora el Grupo A) tendrá una metodología más tradicional, siguiendo el temario tal como se presenta en el libro. El otro grupo (a partir de ahora el Grupo B) será el que tenga la metodología manipulativa. Al finalizar el tema, a ambos grupos se les pasará una prueba final, diferente a la inicial, pero con dificultad similar.

3.4. Diseño de la acción

Las actividades manipulativas llevadas a cabo son las siguientes:

• Crear una balanza:

El primer paso es preparar todo el material: cortaremos el cordel en 4 trozos iguales. 2 trozos serán para un envase y los otros dos para el otro envase. Extendemos un trozo de cordel y a la mitad pegamos la parte inferior del envase. Hacemos lo mismo con otro trozo, pero cruzado de forma perpendicular con el anterior. De esta forma, de todos los lados del envase saldrá un trozo de cordel. Repetimos esto con el otro envase y los otros dos cordeles.

Cogemos la percha y en uno de sus extremos se cuelga el envase, ponemos celo para fijar los cordeles a la percha. Repetimos con el otro envase en el otro lado de la percha. Los envases deben quedar a la misma altura.

• Experimentar con la masa:

Utilizaremos el propio estuche de los alumnos. Primero ellos deben de hacer una estimación sobre el peso de los accesorios que tienen en su estuche. Deberán colocarlos de mayor a menor peso, según ellos crean. Una vez que lo han hecho, comprobarán si su estimación es correcta comparando los objetos con la balanza que ellos mismos han creado. Si se han equivocado deberán utilizar la balanza para ordenar correctamente los objetos.

Dejaremos a los alumnos que experimenten con los objetos que tienen en el estuche y hagan estimaciones y pruebas. Por ejemplo, qué pesa más, el sacapuntas y el pegamento o la goma y el bolígrafo.

• Jugamos con la estimación:

En gran grupo se escogerán varios alumnos y escribiremos sus nombres en la pizarra. Pediremos a todos los alumnos que respondan a las siguientes preguntas en su cuaderno usando la estimación:

• ¿Quién pesa más, X o Z?
• ¿Quién pesa menos, X o T?
• ¿Quiénes pesan menos juntos, TY o XZ?
• ¿Cuánto crees que pesa cada uno?
• Ordénalos de menor a mayor peso.

Después de unos minutos, pesamos a los alumnos que están apuntados en la pizarra y escribimos su peso. Una vez que tenemos todos los datos podemos empezar a comprobar las estimaciones que han hecho los alumnos y responder correctamente a las preguntas anteriores.

 En el momento de realizar la actividad fue interesante dar en un principio solo el peso real del primer alumno y dejar que los alumnos le dieran significado puesto que las estimaciones estaban bastante alejadas de la realidad, tanto por encima como por debajo. Así hicimos la variante de que dijeran cuánto creían que pesaba el siguiente alumno y comprobar quién se había acercado más. Fue una buena forma de darle significado a los kilos que pesa una persona. Puesto que, a partir de la primera medición, las estimaciones fueron mucho más cercanas a la realidad.

• Utilizamos diferentes unidades según lo que queremos medir:

Aprovechamos esta actividad para introducir la tabla de equivalencias de masa.

Con la báscula de suelo pedimos a los alumnos cuánto pesa un estuche. Pedimos que un alumno compruebe el peso ambas básculas. La de cocina nos dará un peso exacto mientras que la de suelo es posible que no llegue a pesarlo o que sea inexacto. De esta forma los alumnos podrán comprobar que según lo que queremos pesar necesitaremos usar una unidad u otra.

Ahora es el momento de introducir todas las equivalencias del Kg y después experimentaremos pesando qué unidades necesitaremos según el objeto que sea. Podemos pesar libros, mochilas, estuches, etc.

Con esta actividad pueden empezar a pasar de forma compleja a incompleja y comprobar con la báscula el resultado. El profesor pesará algún objeto de la clase y dictará a los alumnos el peso en forma compleja, los alumnos deberán pasar a la forma incompleja y una vez hayan terminado se acercarán a la báscula para pesar el objeto y comprobar si han hecho correctamente el cambio.

Esta actividad se realizará con varios objetos diferentes para que los alumnos puedan practicar.

• Sumas y restas con la báscula:

Le diremos a los alumnos el peso de dos objetos diferentes del aula y deberán calcular cuánto pesan juntos. Una vez realizado, se comprobará con la báscula el resultado de la suma.

Podemos dar el peso total de dos objetos juntos y lo que pesa uno de ellos para que ellos tengan que averiguar el peso del otro objeto.

Otra variedad sería decir una cantidad máxima que puede pesar una mochila y el peso que tiene ahora esa mochila, ellos deberán calcular la cantidad de peso que aún pueden meter. Después lo podrán comprobar con la báscula.

3.5. Análisis de datos e interpretación de resultados

A continuación, se presentan varias tablas con los resultados obtenidos con las pruebas iniciales y finales que han realizado los dos grupos. Una vez insertados en una tabla estadística y calculadas la media y la desviación típica, se considera que son bastante representativas como para poder presentarlas por sí solas. Recordemos que el Grupo A es el que siguió la metodología tradicional y el Grupo B es el que siguió la metodología innovadora.

Tabla 1. Resultados de las pruebas

Si se analiza la media y la desviación típica reflejadas en la tabla 1 se observa que: en el Grupo A la media aumenta de 2.8 hasta 5, por lo que queda claro que la instrucción ha tenido efecto sobre el grupo. Además, las desviaciones son similares tanto en el test inicial como en el final, por lo que son razonablemente comparables entre sí.

En cuanto al Grupo B, se observa lo mismo que en el Grupo A, pero con una mejora mucho más notable, puesto que pasan de un 2.7 (prácticamente la misma nota inicial que el Grupo A), hasta un 7. Las desviaciones en este grupo también son del mismo valor y, por lo tanto, las medias, antes y después, son comparables y significativas.

Además, las deviaciones típicas de los dos grupos son muy similares, por lo que también podremos comparar con fiabilidad los resultados obtenidos entre los test iniciales y finales de un grupo y de otro.

Tabla 2: Porcentajes de los resultados

Respecto a los porcentajes, se han representado en la tabla 2 las calificaciones extremas. En muy deficiente están los alumnos que no han superado el 3 y en notable se han incluido a los que han superado el 7.

Se puede ver claramente que, antes de la instrucción, ambos grupos se encuentran prácticamente en la misma situación de partida. En el Grupo A, el 67% de los conocimientos de los alumnos son muy deficientes, un resultado muy parecido al Grupo B, en el que hay un 65% de alumnos en este intervalo. En cuanto a los alumnos con nota superior al 7, también son los mismos resultados, un 6% para el Grupo A y un 5% para el B.

Sin embargo, una vez llevada a cabo la acción innovadora, los resultados no son tan parecidos. Es cierto que en los dos grupos ha habido una mejoría, pero en el Grupo B es donde ha habido una mayor evolución. En el Grupo A aún quedan un 18% de los alumnos por debajo del 3 mientras que en el Grupo B se ha reducido el número de alumnos con conocimientos muy deficientes a un 5%.

Pero lo que hay que destacar es el número de alumnos por encima del notable: así como en el Grupo A ha aumentado hasta un 28%, en el Grupo B nos encontramos el 60%, casi dos tercios de la clase, con más de notable.

En Grupo B se puede decir que los porcentajes se han girado respecto del control inicial al final. Pasando de un 5% a un 60% de notables y de un 65% de suspendidos inicialmente a un 5% tras la formación. Por lo que, se observa claramente que, la metodología manipulativa ha dado mejores resultados que la metodología tradicional.

Vamos a ver ahora los resultados más detallados de cada uno de los grupos antes y después de la formación.

Aquí se puede ver de una forma más visual la transformación que ha habido en el Grupo A. Queda constancia de que la formación tradicional ha funcionado.

Antes de la formación, se ve un declive de resultados hacia el aprobado, la media, 2.78, es representativa puesto que la mayoría de los alumnos están por debajo del 3 y ninguno llega al sobresaliente. Sin embargo, tras la formación, los resultados se expanden por todas las calificaciones, aún queda un número elevado de alumnos que no llegan al aprobado, pero también hay bastantes alumnos que sí lo superan, por lo que la media queda en un 5 y también es representativa de los resultados obtenidos.

Los alumnos con necesidades educativas especiales de este grupo no superaron los test en ninguno de los casos.

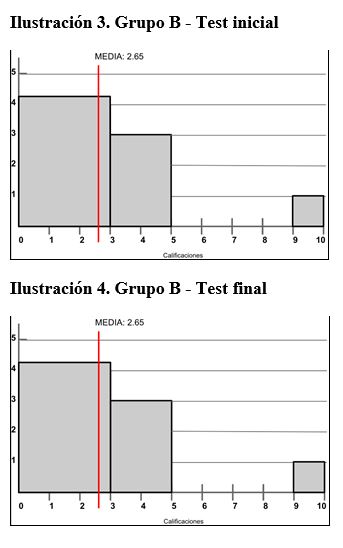
En cuanto al grupo B, el cambio ha sido mucho mayor respecto del control inicial al final.

En la figura 3 se observa como prácticamente la totalidad del alumnado estaba suspendido en la prueba inicial, estando la mayoría por debajo del 3. La media, en este caso, no es representativa al 100%, puesto que el alumno que ha aprobado con sobresaliente esta prueba aumenta la media (considerado valor atípico). Por lo que la media real de este grupo debería ser algo más baja de la que sale.

Ya que un valor atípico es un dato que es considerablemente diferente a los otros datos de la muestra, con frecuencia, pueden alertar a los estadísticos sobre las anormalidades experimentales o los errores en las mediciones tomadas, y debido a esto se pueden descartar del conjunto de datos. Si los valores atípicos del conjunto se ignoran, puede haber cambios importantes en las conclusiones obtenidas del estudio. Aun así, se ha preferido mantener todos los datos que se han obtenido para que no distorsionar la realidad que se ha dado.

El dato a destacar es el cambio de media que ha habido respecto de la prueba inicial a la final, puesto que la media final roza el notable. Se puede observar en la figura 4 que las calificaciones están más espaciadas quedando la moda en notable y siendo bastante superior el número de alumnos que han aprobado a los que no.

Además, lo más curioso es que los alumnos de necesidades educativas especiales sí que superaron el test o se quedaron muy cerca del aprobado. Por lo que, además, se puede añadir que una propuesta manipulativa no tiene porqué ser adaptada para alumnos con necesidades y pueden participar con su mismo grupo de iguales llegando a conseguir casi los mismos resultados que el resto.

Echando un vistazo a los resultados de los test iniciales: Las desviaciones, como se ha visto en la tabla 2, también son muy parecidas, por lo que permite poder comparar los resultados obtenidos entre ellos con fiabilidad. Además, se ve que ambas medias están entre el 2.5 y el 3.

Esto significa, sin duda, que la situación de partida en ambos grupos es exactamente la misma. Por lo que los cambios que se producen tras las dos diferentes metodologías son perfectamente comparables.

En cuanto a los resultados finales de ambos grupos, como se ha dicho anteriormente, en los dos grupos la formación ha sido útil, puesto que se ha producido aprendizaje en ambos. La media ha subido en los dos, pero la evolución ha sido mucho mayor en el Grupo B, tal y como se observa en la Ilustración 4. En los dos grupos hay de todo tipo de calificaciones, aunque en el Grupo A, gran parte de alumnos siguen sin llegar al aprobado. Sin embargo, en el Grupo B, la mayor parte de los alumnos están por encima del notable.

Conclusiones

A lo largo del trabajo, hemos desarrollado diversos conceptos que nos hacen comprender los niveles de adquisición del proceso de medida y las diferentes etapas que pasan los niños hasta que consiguen tener un significado de la unidad de medida. Además, también hemos visto cuales son los pasos para la constitución de la unidad.

Debido a esto, es necesario ofrecer una educación de calidad a todos los estudiantes, adaptándola a sus diferentes capacidades, características, necesidades, estilos y ritmos de aprendizaje e intereses, por tanto, la necesidad de hacer una mejora en cuanto a los materiales que se utilizan, que se adaptase a todos los estudiantes y niveles es imprescindible para poder brindar la posibilidad de una educación completa a todos los alumnos por igual. Utilizando una metodología manipulativa, lograremos un progreso óptimo de las potencialidades de cada estudiante en todas sus áreas de desarrollo cognitivo.

Con la puesta en marcha de las actividades propuestas se ha podido demostrar que los resultados que se obtienen son mucho mejores dejando que los alumnos manipulen, jueguen y experimenten. De esta forma, los alumnos aprendieron matemáticas sin darse cuenta de que lo estaban haciendo, puesto que para ellos eran juegos en todo momento. Este es un punto fuerte de la propuesta, puesto que dejamos de lado los bloqueos ante un área que suele crear bastantes barreras.

A pesar del avance en las técnicas de desarrollo de las capacidades cognitivas de los alumnos, todavía queda un largo camino que recorrer, pero para que este avance sea significativo es necesario adaptar los materiales escolares y las formar de actuar dentro del aula a las necesidades de los alumnos.

Referencias

Libros:

• Ander-Egg, E. (2003). Repensando la Investigación-Acción-Participativa. Grupo editorial Lumen Humanitas.
• Cascallana, T. (1988). Iniciacion a la matemática. Materiales y recursos didácticos. España: Santillana.
• Castro, E. (2001). Didáctica de la matemática en la Educación Primaria. España: Síntesis.
• Chamorro, M. (2005). Didáctica de las matemáticas. España: Pearson Educación SA.
• Chamorro, M. (1988). El problema de la medida didáctica de las magnitudes lineales. España: Editoria Síntesis.
• Elliott, J. (2000). La investigación-acción en Educación. Ediciones Morata.
• Godino, J. (2002). Matemáticas y su didáctica para maestros. Granada: Universidad de Granada.
• Latorre, A. (2003). La investigación acción. Conocer y cambiar la práctica educativa. España: Ed. Graó.
• Puente, G. (1982). El Sistema Métrico Decimal. Su importancia e implantación en España. Madrid: Universidad Complutense.

Revistas:

• Bauselas, E. (2004). "La docencia a través de la investigación-acción". Revista Iberoamericana de Educación, ISSN 1681-5653.
• Blanco, B., & Blanco, L. J. (2009). Contextos y estrategias en la resolución de problemas de primaria. Números, 71, 75-85.
• Fernández, J. A. (2006). Algo sobre resolución de problemas matemáticos en Educación Primaria. SIGMA, 29, 29-42.