Sin embargo, los juegos no son únicamente útiles para motivar a nuestros alumnos, sino que pueden ser un complemento importante para reforzar tareas. Por ello, enumeraremos una serie de ideas para adaptar juegos conocidos y utilizarlos como herramientas en la asimilación y el repaso de ciertos contenidos.
Palabras clave
Matemáticas, recreativas, lúdica, juegos, secundaria.
One of the biggest problems we face when entering a high school classroom to teach mathematics is the rejection, not only of the students, but of society at large, to the subject. Therefore, a good option to end the stereotype of difficult and boring mathematics would be to show their side more interesting and even fun. To this end, we will present some of the games that can help us in motivating students.
However, games are not only useful to motivate our students, but can be an important complement to strengthening tasks. Because of this, we will list a number of ideas to adapt known games and use them as tools in the assimilation and review of certain contents.
Keywords
Mathematics, recreational, playful, games, secondary.
1. Actividades recreativas
En el siglo XVII, apareció el primer libro en el que se recopilaron problemas considerados de matemática recreativa, Problèmes plaisants, de Bachet de Méziriac, cuya primera edición apareció en 1612. A pesar de que anteriormente, obras destinadas a la formación matemática de jóvenes, recogen problemas no utilitarios (sin contexto), sino con un carácter que podríamos considerar lúdico y que, hoy día, aparecen, a veces con ligeras modificaciones, en obras recreativas y en concursos de matemáticas. Entre estas obras, podemos mencionar el papiro de Ahmes, también conocido como papiro Rhind, en tiempos egipcios; las obras escritas por Alcuino de York en el siglo VIII, entre las que destaca Propositiones ad Acuendos Juvenes, una colección de cincuenta y tres problemas recreativos, donde aparece el famoso problema del barquero, el lobo, la cabra y la col; y el Liber Abaci de Fibonacci en el siglo XIII. Es precisamente a principios del siglo XIII, cuando aparecen en Italia las primeras competiciones matemáticas.
Hoy en día, existen las llamadas Olimpiadas Matemáticas Internacionales (OIM) que adquirieron su forma actual en las competiciones W. L. Putnam, organizadas en EE.UU. y Canadá, en 1938. El nombre de “Olimpiadas” data de 1959, año en que se celebraron las primeras Olimpiadas Matemáticas Internacionales en Rumanía, organizadas por Hungría, para alumnos de Enseñanza Secundaria. España se añadió como participante en 1983. Más tarde, comenzaron a realizarse concursos de ámbito regional.
Pero esta no es la única forma en que podemos encontrar actividades recreativas dirigidas a alumnos de secundaria. La matemática lúdica está presente en las aulas en diferentes formas y con distinta finalidad.
Podemos destacar una serie de características de las cuales depende el carácter recreativo de un problema. Los alumnos perciben un problema como lúdico cuando se les presenta en forma de pasatiempo, cuando se sitúa en un contexto cercano a ellos o aparecen personajes que llaman su atención, cuando en la actividad interviene material manipulativo (palillos, fichas de dominó, etc.), cuando se les propone como un desafío, cuando el resultado se contradice con la intuición también suele llamar su atención y, por supuesto, cuando se les presenta en forma de juego con una serie de reglas e, incluso, diseñado a partir de juegos cuya estructura, por lo general, ya conocen (barajas de cartas, juego de La Oca, etc.).
En la actualidad, son múltiples las herramientas digitales que se nos ofrecen para el estudio y la comprensión de las matemáticas. Las páginas web con ejercicios interactivos son un recurso ideal para captar la atención del alumnado, a la vez que fomentan la competencia digital. Alumnos que no realizan las tareas diarias, cuando se les presenta el mismo ejercicio desde la pantalla de un ordenador, sí que muestran interés por resolverlo.
Ejemplo: pedir a nuestros alumnos que calculen el área de una figura puede resultar un ejercicio más atractivo si se presenta de la siguiente manera.
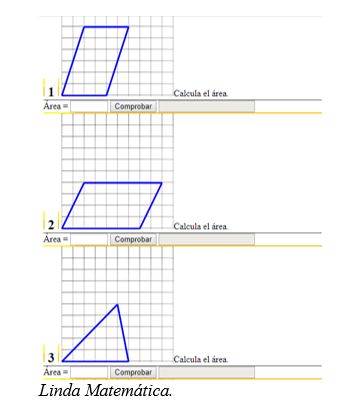
Por otro lado, no debemos perder de vista dos herramientas fundamentales en el estudio de las matemáticas y que nunca quedarán obsoletas con el paso de los años: el lápiz y el papel. El simple hecho de explicarles cómo resolver un sudoku o un cuadrado mágico puede despertar su interés. El sudoku es un juego de estrategia que mejora su capacidad de razonar, mientras que con el cuadrado mágico practican, además, el cálculo.
Ejemplo: cuadrado mágico aditivo. En este, en concreto, les proporcionamos el cuadrado vacío y consiste en colocar los números del 1 al 9 de manera que cada fila, columna y diagonal sume lo mismo.
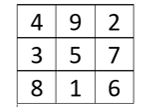
Precisamente, para aumentar la agilidad en el cálculo mental, se pueden utilizar ciertos juegos de magia. Son aquellos en los que se debe de pensar un número y realizar una serie de operaciones, para que ‘el mago’, finalmente, ‘adivine el número’.
Ejemplo: el mago (el profesor) le pide a una persona del público (un alumno o un grupo) que siga los siguientes pasos:
1. Piensa un número.
2. Multiplícalo por cinco.
3. Súmale uno.
4. Multiplica el resultado por dos.
5. Réstale doce.
6. Divide todo entre diez.
7. Resta el número que pensaste.
Finalmente, el mago adivinará el resultado que será siempre -1.
Existen problemas históricos que agudizan el ingenio y el uso de estrategias. Se les suelen presentar como adivinanzas, característica que los hace más atractivos. Éste sería el caso del problema mencionado anteriormente del barquero, el lobo, la cabra y la col.
Ejemplo: Un barquero quiere cruzar el río con un lobo, una cabra y una col. La única manera de cruzarlo es con una barca en la que solo cabe él y el lobo, o él y la cabra, o él y la col. Por supuesto, no se atreve a dejar al lobo solo con la cabra, ni a la cabra sola con la col. ¿Cómo cruzarán el río?
Tampoco debemos olvidarnos de los juegos en los que aparecen otro tipo de materiales que el alumno puede manipular como, por ejemplo, aquellos en los que intervienen palillos, el tangram o modificaciones de juegos de cartas o el dominó.
Ejemplo: ¿Cómo podemos formar cuatro triángulos equiláteros iguales con seis palillos?
Estos materiales son fáciles de conseguir e incluso se pueden fabricar con cartón o papel plastificado. Este hecho puede ser una de las ventajas que tienen estos juegos frente a las herramientas digitales, puesto que, dependiendo del nivel socio-económico de las familias, no todos nuestros alumnos pueden permitirse dispositivos digitales, como un ordenador o una tablet.
2. Variantes
Tal y como hemos comentado al comienzo del artículo, la mayoría de estos juegos se pueden modificar de acuerdo a nuestras necesidades. Es posible adaptarlos a los distintos bloques de contenido, así como al nivel con el que estamos trabajando.
Veamos, a continuación, algunas variantes que pueden ser de utilidad, o bien, servir de inspiración para muchas otras.
- Cuadrado mágico:
En esta modificación del cuadrado mágico, trabajaremos con números enteros. Les daríamos el cuadrado sólo con la casilla del centro y tendrían que conseguir que todas las filas, columnas y diagonales sumen 0.
Tienen que llegar a la conclusión de que la forma de completarlo es colocar cada número con su opuesto, tal como aparece en la imagen.
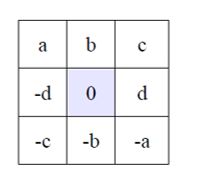
De este modo, conseguiremos que manejen números enteros y asimilen la definición de opuesto de un número.
Otra adaptación sería utilizar como elementos del cuadrado mágico polinomios, en lugar de números, si lo que queremos es repasar las operaciones entre ellos.
En el siguiente ejemplo, les presentamos a los alumnos el cuadrado mágico, con los tres datos que aparecen en las casillas azules y la constante mágica y ellos deben completar el resto.
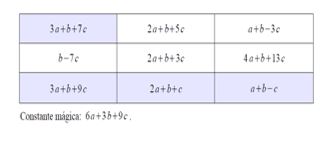
- Magia:
En el caso del juego de magia, nos basta con cambiar los números, el resultado final o las operaciones que vamos realizando, teniendo la precaución de deshacerlas después. El objetivo, sin embargo, continuaría siendo el mismo: mejorar el cálculo mental.
El profesor pide a los alumnos que sigan los siguientes pasos:
- Piensa un número.
- Multiplícalo por tres.
- Súmale uno.
- Multiplica el resultado por dos.
- Réstale ocho.
- Divide todo entre seis.
- Resta el número que pensaste.
Finalmente, el mago adivinará el resultado que será siempre -1.
Estos juegos, normalmente, les suelen provocar mucha curiosidad, ya que saben que, sin duda, tiene truco e intentan averiguarlo. Por ello, puede ser interesante también introducirlos en temas del bloque de álgebra. Presentando diferentes variaciones del mismo juego, como la que acabamos de hacer, advertirán que se sigue un mismo patrón y algunos de ellos llegarán a una fórmula o expresión algebraica.
- Dominó:
Para este tipo de juegos (dominó, oca, cartas...) habría que distribuir a los alumnos por grupos. En este caso, grupos de cuatro, dos parejas, una contra la otra. Así, estaríamos fomentando el trabajo en equipo y la deportividad, ya que habrá una pareja vencedora y los vencidos deberán encajar esa situación. Para controlar las reacciones negativas, es conveniente que las parejas o equipos vayan cambiando en las distintas sesiones que se realicen. Además, intentaremos repartir a los alumnos de manera que haya un cierto equilibrio entre las parejas, para que no haya una diferencia demasiado grande en los resultados.
Antes de empezar, deberíamos de explicar las reglas del juego. Tomaríamos solo algunas de ellas, ya que muchas no son relevantes para nuestro propósito y, sin embargo, pueden resultar complicadas de asimilar para los alumnos que no hayan jugado nunca.
Consistirá en formar las veintiocho fichas de dominó colocando algunas funciones fundamentales, como la exponencial, logaritmo neperiano, trigonométricas, etc. Por ejemplo, en lugar del punto que representa al número 1, colocamos la función ‘ln x’; en otra ficha, en el lugar del 1, ponemos la gráfica de dicha función; en otra ficha que deba contener al 1, ponemos una propiedad de la función... Y así lo haremos con todas las funciones seleccionadas.
Como se puede deducir de lo anterior, trabajaremos con siete funciones distintas, puesto que las fichas de dominó contienen la representación de los números del 0 al 6. Para colocar las piezas, debe coincidir que uno de los extremos de la ficha que está en el tablero, tenga una propiedad referente a la función que tenemos en la ficha que queremos poner o deducir cuál es esa función y colocar la ficha que contenga otra propiedad de la misma.
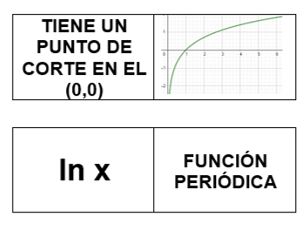
En este ejemplo, podríamos unir las dos fichas que aparecen, puesto que la gráfica es la del logaritmo neperiano, ln x.
Determinaremos quién empieza el juego utilizando un dado: el que saque la puntuación más alta será ‘el mano’ y el que esté sentado a su derecha será quien empiece la partida. Al igual que en el dominó original, el sentido de juego será hacia la derecha y los miembros de cada pareja se sentarán uno frente al otro. La mano terminará cuando uno de los miembros de la pareja haya colocado todas sus fichas o se produzca el cierre. Por cada mano, la pareja ganadora obtendrá tres puntos y si se produce empate, un punto para cada pareja. Podríamos seguir jugando toda la sesión, sin límite de puntos.
En cuanto a los materiales que podemos utilizar, pueden ser muy diversos. Lo más sencillo sería utilizar cartulinas blanca y negra para la parte anterior y posterior de las fichas, respectivamente. Al fabricar de esta manera las fichas, tendríamos la ventaja de hacerlas del tamaño que nos interese, más grande para que se lean mejor las propiedades. Un problema que nos surge es que, en lugar de fichas, obtendremos algo más parecido a cartas y no se sostendrán en pie, pero podemos colocarlas boca abajo en la mesa.
Esta adaptación es útil para reconocer funciones y repasar sus propiedades. Pero se pueden hacer muchas otras con números, operaciones que tengan el mismo resultado, ecuaciones equivalentes, etc.
De hecho, podríamos hacer una adaptación tan sencilla como colocar en cada extremo de la ficha una multiplicación de números naturales, teniendo en cuenta que contaremos con sólo siete resultados distintos. Es un problema bastante frecuente, encontrarnos alumnos en la etapa de secundaria que no saben las tablas de multiplicar, quizá por el uso abusivo de la calculadora. Algo tan básico es de suma importancia para que los estudiantes consigan los objetivos de su etapa, puesto que no podemos pretender que realicen correctamente multiplicaciones con números enteros, decimales, fracciones o polinomios si no conocen las tablas. Sin embargo, no podemos ocupar nuestro tiempo en contenidos correspondientes a la etapa de Educación Primaria.
Por ello, y dada la sencillez del diseño del juego, así como el bajo coste de los materiales, se les puede proponer que fabriquen uno en casa para jugar con amigos y familiares. Se les comentaría que no es necesario formar parejas, ya que puede resultar complicado conseguir cuatro participantes, es suficiente jugar uno contra uno.
3. Momentos
Después de todas estas ideas y conociendo el tiempo del que disponemos los docentes para impartir todos los contenidos y, así, cumplir los objetivos propuestos, es natural que surja la pregunta: ¿cuándo introducimos estos juegos en el aula?
Pues bien, hay diversos momentos en los que podemos dirigir la atención de nuestros alumnos hacia la matemática lúdica.
Los ejercicios interactivos se pueden introducir en nuestra programación didáctica, dedicando, por ejemplo, una sesión a la semana o cada dos semanas a visitar el aula de informática del centro. Así, al introducir las actividades en las horas lectivas, los alumnos podrán disponer de los recursos necesarios, ya que, para algunos de ellos, puede que sea imposible llevar a cabo estas actividades en casa.
Los más rápidos, como acertijos o juegos de magia, se pueden lanzar al aire al finalizar una clase. En especial, en esas ocasiones en que nos sobran unos minutos, pero no es suficiente para explicar un apartado nuevo. Si les queremos hacer pensar un poco más, podemos darles la respuesta al día siguiente, al comienzo de la clase.
En cuanto a los juegos de cartas o el dominó, es evidente que nos llevarán más tiempo. Deberíamos dedicar una sesión completa a ellos. Por ello, no será posible introducirlos de manera frecuente.
Los sudokus, así como los cuadrados mágicos, se resuelven de manera individual, por tanto, se pueden proponer para casa. Será una buena forma de aportarles un nuevo pasatiempo, alejado del abuso de las tecnologías que sufrimos hoy en día. Incluso, se pueden complementar si les decimos que busquen ellos otros parecidos en Internet. En este caso, sería conveniente recomendarles nosotros mismos las páginas en las que pueden encontrarlos.
En ocasiones, como ciertas festividades o eventos, por ejemplo, la semana cultural, se organizan actividades fuera del aula. Estos días son ideales para organizar gymkanas y juegos similares, por ejemplo, un scape room matemático. En este último, los alumnos deberán de superar una serie de pruebas relacionadas con las matemáticas para descifrar los códigos de los candados y poder, así, ‘salir’. No es necesario encerrarlos, simplemente, cuando abran el último candado se encontrarán con una nota que diga: ‘¡Lo habéis conseguido, estáis fuera!’. Las pruebas que deban realizar pueden ser una combinación de las actividades que hemos mencionado anteriormente. Por ejemplo, la resolución de un cuadrado mágico al que le falten tres o cuatro elementos que coincidan con el código de uno de los candados. Incluso pruebas cuyo resultado nos conduzca a otra prueba, como la resolución de un juego de magia y que el número obtenido esté presente en una caja o estantería donde encuentren otra prueba (en este caso, el juego debería de tener un resultado constante, de manera que todos los participantes obtengan el mismo número y se corresponda con el que nosotros hemos colocado).
Conclusiones
El artículo pone de manifiesto el uso de las actividades recreativas no sólo como elemento motivador, sino como un recurso interesante ante procedimientos matemáticos rutinarios que, pueden resultar tediosos para los alumnos. También, incluye ejemplos como muestra de las actividades que se pueden realizar en el aula, los cuales admiten modificaciones, tal y como hemos visto.
Además, es importante la insistencia en que no son actividades cerradas. Aunque hemos mostrado algunos ejemplos de modificaciones, la idea del artículo es que los profesores que lo lean debe ser capaces de adaptar e incluso diseñar juegos y actividades de este tipo, que puedan ser un recurso útil para sus alumnos, teniendo en cuenta las necesidades de cada grupo al que van dirigidos.
Mi experiencia personal en la puesta en práctica de estas actividades ha sido, generalmente, positiva. Este tipo de actividades no sólo nos ayudan a captar la atención de nuestros alumnos y motivarlos, sino que son adicionalmente un buen recurso para asimilar tanto contenidos, como técnicas. Cuando aprendemos algo porque nos ha sorprendido o nos resulta entretenido, queda más fácilmente grabado en nuestra mente y por más tiempo.
Por último, apuntar que el desarrollo de algunos temas que aparecen aquí, da lugar a la consideración de las posibilidades de la matemática lúdica como el trabajo de técnicas, el diseño de planificaciones didácticas que incluyan juegos matemáticos y actividades lúdicas, o el estudio de las actividades que aparecen en Olimpiadas y otros concursos. La profundización en cada uno de estos temas daría lugar a un artículo en sí.
Referencias
- Federación Española de dominó. (2017): Reglamento del juego y competiciones. Madrid.
- Linda matemática. 22-10-2019 en https://sites.google.com/site/weblindamatematica/
- MCN biografías.com. Alcuino de York (735-804). 22-10-2019 en https://www.mcnbiografias.com/app-bio/do/show?key=alcuino-de-york
- Murcia, J. A. (2016): El truco que adivina tu edad y tu talla de zapato no es magia, sino matemáticas. 22-10-2019 en https://verne.elpais.com/verne/2016/01/22/articulo/1453461713_812958.html
- Olimpiada Matemática Internacional. 22-10-2019 en http://www.imo-official.org
- RSME Olimpiada Matemática Española (2007). 22-10-2019 en https://www.olimpiadamatematica.es/platea.pntic.mec.es/_csanchez/olimpque.htm
- Sánchez, E. (2011): La matemática lúdica en el aula. Ponencia invitada, 15 JAEM, Jornadas sobre el Aprendizaje y la Enseñanza de las Matemáticas. Gijón, Asturias. En prensa.

