Educación infantil: competencia matemática a través del juego, del arte y de la literatura

La respuesta podría ser prácticamente infinita, ya que gracias a estas herramientas ponemos al alcance de todos los alumnos y alumnas los recursos necesarios para que desarrollen todo tipo de competencias y contenidos curriculares.

En este artículo intentaremos dar respuesta a estas cuestiones centrándonos en el juego, el arte, la literatura y las tareas o situaciones problema que esconden implícitamente los juegos como recursos privilegiados para el desarrollo de la competencia matemática.

Palabras clave

Competencia matemática, trabajo por tareas, representaciones artísticas, cuentos, juegos.

Most of society think that child come to infant school only singing songs, paint, play games or listening tales. But, do we really know what are we developing through playing games, making plastic works or through the literature? Which objectives are we working through them? How can we work the different curricular contents with these resources?

The answer to these questions could be infinity because thanks to these tools children can develop all kinds of competences and curricular contents.

On this article, we try to answer the previous questions, focusing on children games, art and literature to develop mathematical competence.

Keywords

Mathematical competence, work of tasks, plastic works, tales, games.

La competencia matemática en la vida diaria y en Educación Infantil

Como dijo John Allen, “la vida es matemática”. Las matemáticas están por todos los lados: las podemos ver cada mañana al despertar, las podemos tocar con las manos y sentir a través de los sentidos. Las utilizamos continuamente a penas sin prestar atención y, como no, también las podemos encontrar en los cuentos infantiles, las canciones, las obras de arte o en cualquier tipo de juego que realicemos. Tan solo necesitamos un poco de imaginación y se convertirán en recursos privilegiados para el aprendizaje de contenidos matemáticos.

La formación matemática que permite a los individuos enfrentar con éxito los problemas de la vida cotidiana depende, en gran medida, de los conocimientos adquiridos y de las habilidades y actitudes desarrolladas durante la Educación Básica. La experiencia que vivan los alumnos al estudiar matemáticas en la escuela puede traer como consecuencia, el gusto o el rechazo hacia la disciplina, la creatividad para buscar soluciones o la pasividad para escucharlas y tratar de reproducirlas.

1. ¿Cómo relacionar las matemáticas con el arte?

¿Qué pintan Picasso, Miró o Kandinsky en una propuesta de Educación Infantil? Una de las respuestas podría ser: ¡matemáticas! Aunque las matemáticas y el arte pueden concebirse como dos disciplinas opuestas, las representaciones artísticas en cualquiera de sus formas son un excelente recurso para acercar a los estudiantes a los principales conceptos matemáticos como las relaciones espaciales y la geometría de una forma visual e innovadora.

La maestra y Doctora en Didáctica de las matemáticas Mequé Edo, propone que uno de los contextos adecuados para la enseñanza y aprendizaje de nociones matemáticas es la contemplación y posterior creación de formas artísticas. Las representaciones artísticas pueden ayudar al alumno tanto a intuir nociones geométricas como a desarrollar sentimientos y emociones estéticas, entender procedimientos, valores o actitudes relacionadas con la competencia matemática.

De este modo, mediante la contemplación de obras pictóricas, lograremos la comprensión del concepto de semejanza, diferencia, geometría, prismas dimensión, perspectiva, simetría, líneas, cortes entre superficie o planos, entre otros. Y, mediante la creación de obras plásticas a través de diferentes técnicas, daremos forma a nuestro pensamiento lógico-matemático

1.1 Aplicaciones didácticas

En resumen, para trabajar la competencia matemática se pueden desarrollar numerosas actividades teniendo en cuenta obras pictóricas o esculturas de nuestro entorno. A continuación, se presentan una serie de contenidos matemáticos y una batería de actividades para desarrollarlos:

Estudiar las formas y líneas básicas: para iniciar a los más pequeños durante la etapa de Educación Infantil en estos conceptos matemáticos básicos, la maestra y doctora en Didáctica de las matemáticas Mequé Edo, propone trabajar con obras que representan las principales figuras planas de un modo evidente, como “bailando por miedo” de Paul Klee o “composición VIII” de Kandinsky, entre otras. La tarea del alumno consiste en analizarlas, cuantificarlas o estudiar su situación espacial en el cuadro.

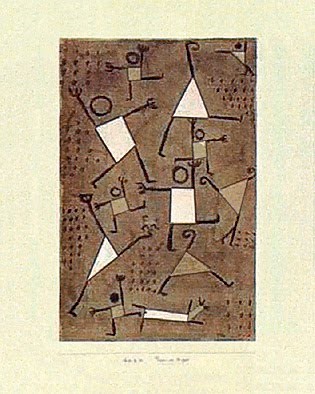
Bailando por miedo de Paul Klee.

Tras reflexionar en gran grupo sobre las características de la obra, se puede realizar una representación artística inspirada en la misma utilizando consignas como: “En el dibujo hay: 2 cuadrados amarillos, 3 círculos azules y 2 triángulos morados”.

Al finalizar la obra individual creamos un mural donde reunimos las representaciones de todos los alumnos/as.

Representación artística “Bailando por miedo” de los niños y niñas de 5-6 años.

Haciendo uso de la cantidad de obras artísticas que nos brinda nuestro entorno, sobre todo derivadas del arte contemporáneo, cuyos autores utilizan los recursos geométricos en más de una ocasión, seleccionaremos una obra que nos pueda servir como base para el trabajo de observación, análisis y composición.

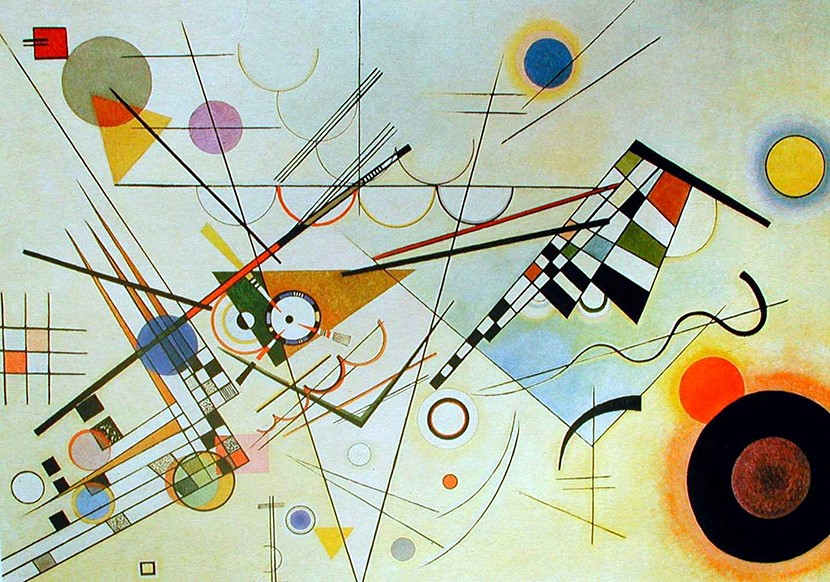
Composición VIII de Kandinsy.

Observaremos el cuadro y jugaremos a identificar sus formas geométricas, líneas, la posición de los objetos en el espacio, y posteriormente realizaremos nuestras composiciones utilizando la técnica plástica que cada uno prefiera para su obra (pintura, plastilina, material reciclado…).

Composición en relieve con materiales de reciclaje realizada por niños de 4-5 años inspirada en la Composición VIII de Kandinsky.

Composición en relieve con plastilina realizada por niños de 5-6 años.

Trabajar con la perspectiva: la profundidad en una pintura se consigue con la perspectiva, una técnica que requiere mediciones y cálculos precisos por parte del autor. En el aula se puede analizar el proceso seguido por los pintores en la creación de sus obras para lograr este efecto, presente de modo latente en algunos cuadros como las Meninas de Velázquez, o La última cena de Leonardo da Vinci. Donde se distinguen claramente el fondo y el primer plano

Las meninas de Velázquez.

A través de su contemplación podemos entender conceptos como; fondo, primer plano, Y podemos sugerir actividades para comprender estos conceptos como reconstruir el cuadro recortando cartulinas y pegándolas para formar el cuadro de las Meninas en versión 3d.

Las meninas de Velazquez de un grupo de 5-6 años.

Dependiendo de la edad y de la madurez del grupo podremos proponer actividades para profundizar en la perspectiva, actividades motivadoras y sugerentes como realizar una carretera con perspectiva tomando como referencia líneas rectas y diagonales.

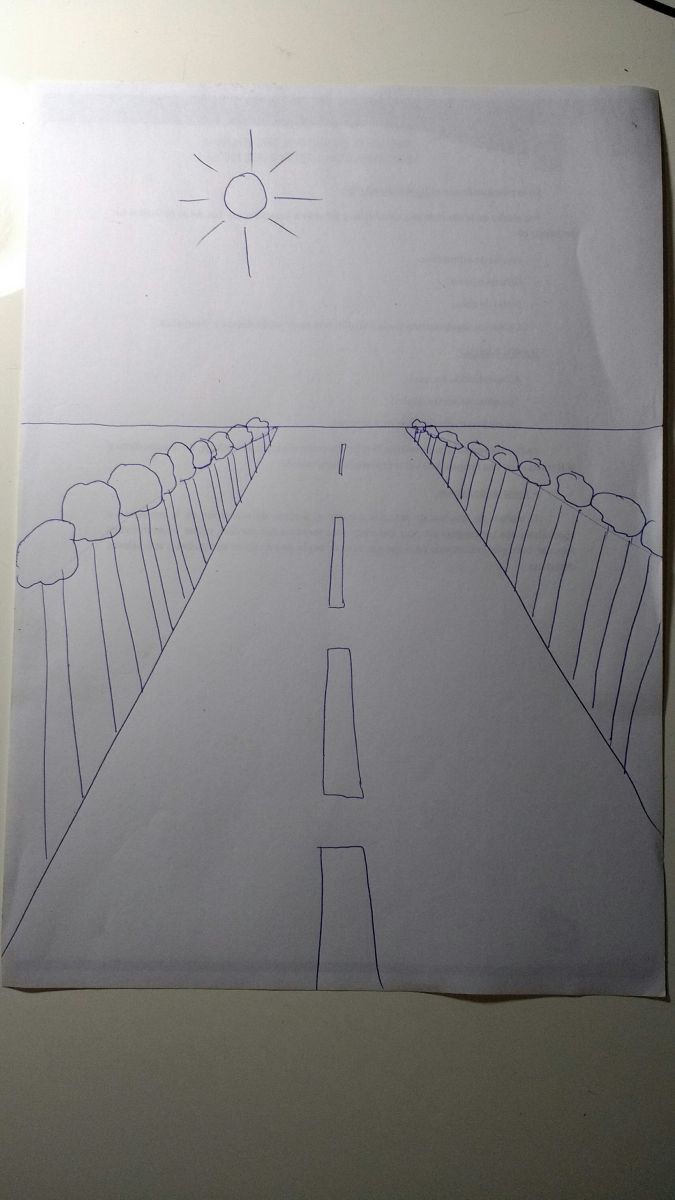
Carretera con profundidad para trabajar fondo y primer plano tras observar las Meninas.

 Otra técnica consiste en constatar falta de perspectiva en otras pinturas (gran parte de las obras del románico) y realizar propuestas para obtenerla.

Imagen de una obra anónima del Románico.

Identificar y analizar las formas geométricas: obras de Picasso, Joan Miró, Kandinsky y otros representantes pueden utilizarse para descubrir diferentes figuras y formas geométricas, así como las relaciones entre ellas. Del mismo modo, la obra pictórica de Escher, en la que el artista juega en muchas ocasiones a esconder y superponer poliedros, ayuda al alumno a mirar con ojos matemáticos más allá de la simple apariencia.

Pintura de Joan Miró.

Posteriormente pasaríamos a realizar una obra plástica inspirada en la obra previamente contemplada y utilizando consignas como: “colores a utilizar: rojo, azul y negro y formas geométricas: círculos y triángulos”, los niños crean su propio Miró a la vez que trabajan conceptos matemáticos como números o formas geométricas.

Grupo del tercer nivel del segundo ciclo de Educación Infantil componiendo su propio Miró a partir de consignas.

Acercarse a los conceptos de proporción, simetría y particiones: “El hombre de Vitruvio” uno de los más famosos dibujos de Leonardo da Vinci, es la representación artística más clara de las proporciones matemáticas y la simetría básica. El alumno puede analizarlo y trabajar sobre algunas de las nociones proporcionales que propone, con la longitud de los brazos extendidos de un hombre, considerada igual a su altura, o desde la punta de la barbilla a la parte superior de la cabeza, estimada en un octavo de su estatura.

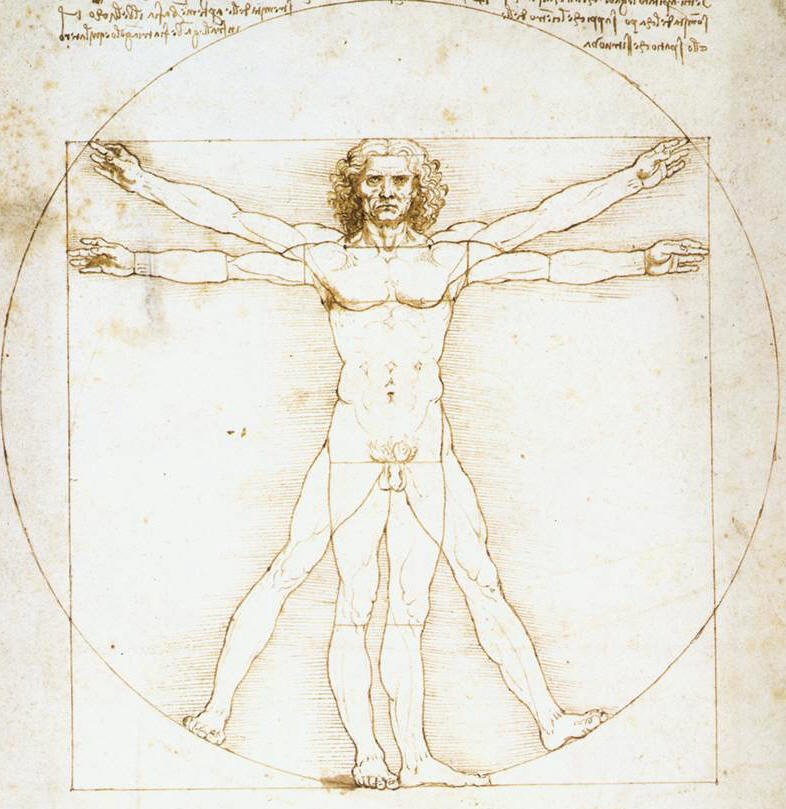
Hombre de Vitruvio de Leonardo.

Escultura del encierro de San Fermines en Pamplona.

Esculturas realizadas por los niños y niñas de 4-5 años con material reciclado tras visitar el monumento del encierro de San Fermines.

2. ¿Cómo relacionar las matemáticas con los cuentos?

No se necesita un cuento específico que trate sobre matemáticas, como hemos dicho al principio, las matemáticas se encuentran por todos los rincones y también, en los cuentos. Todos ellos, o su gran mayoría, vienen paginados con números que siguen un orden ascendente, presentan una serie de hechos ordenados y presentan un número determinado de personajes.

Mediante los cuentos podemos identificar conceptos y realizar reflexiones sobre tamaños (unos personajes son más grades que otros), identificar atributos de elementos o colecciones (por ejemplo, en un cuento que aparezcan animales y personas). Del mismo modo, tras la lectura, se pueden proponer actividades en las que podamos, desde realizar cuantificaciones sencillas hasta clasificar objetos del cuento según atributos.

Los contenidos matemáticos, así como el grado de dificultad de la actividad atenderá siempre a las características psico-ebolutivas de los alumnos y alumnas. Es decir; Mientras que con niños y niñas de 5 años realizaremos breves cuentos, los paginaremos y ordenaremos en secuencias lógicas los ítems de la historia previamente leída, con los niños y niñas de 3 años, bastará con realizar comparaciones entre personajes, cuantificarlos u observar las formas geométricas que aparecen en el cuento.

2.1. Aplicaciones didácticas

A continuación, veremos algunas sugerencias para trabajar la competencia matemática a través de los cuentos.  Podemos relacionar las matemáticas con los cuentos de dos formas: Una vez sepamos el objetivo o contenido que queramos trabajar, buscaremos el cuento que más nos pueda ayudar a desarrollar los contenidos deseados, o bien, podemos partir de un cuento que sea significativo para los niños y utilizando nuestra imaginación encontrar su lado matemático para poder trabajar los contenidos de forma más significativa.

Idea de magnitud y medida: grande, mediano, pequeño: “Los tres cerditos” o “ los tres ositos” (apropiados para 3años).

Cuantificar objetos: Como hemos mencionado anteriormente, todos los cuentos vienen paginados, y con un número determinado de personajes. Se puede comenzar con los más pequeños a cuantificar elementos, personajes, el número de hojas del cuento, número de patas del animal…etc. Con los mayores podremos crear nuestros propios cuentos además de paginarlos.

Identificar atributos de elementos y colecciones: cualquier cuento que contenga grupos de animales, cuentos sobre oficios donde cada uno tenga sus herramientas o vestimenta, nos podrán ayudar como recurso a la hora de identificar atributos de elementos y colecciones.

Cuentos de animales para clasificar según atributos.

Libro sobre profesiones para identificar atributos de elementos y colecciones

Clasificar objetos según atributos. Tras la lectura del cuento se pueden proponer actividades en las que los niños puedan clasificar de forma real y manipulable los objetos que aparecían en el cuento. Clasificamos animales domésticos y salvajes y hacemos un recuento de cuántos animales tenemos en cada grupo.

Clasificación y cuantificación de animales.

3. ¿Cómo relacionar las matemáticas con el juego?

Como bien sabemos los maestros y maestras de Educación Infantil, el juego es la actividad por excelencia del niño y de la niña. Psicólogos y pedagogos coinciden en que es la actividad más importante durante su desarrollo. Así, cualquier contenido matemático que se disfrace de juego será asimilado sin necesidad de esfuerzo o memorización, siendo interiorizado gracias a su impacto emocional.

Dentro del grupo denominado como “juegos” existen diversas categorías y subcategorías donde se encuentran los juegos de mesa, yincanas, juegos que se realizan dentro de la rutina escolar, juegos reglados, etc.  También las tareas o situaciones problema disfrazados en forma de juego servirán como metodología ya que todos ellos abarcan componentes matemáticos.

3.1. Aplicaciones didácticas

Un enfoque por competencias llevado al aula representa un cambio metodológico, puesto que, entre otros, exige trabajar regularmente por tareas o situaciones problema, considerar los saberes como recursos a movilizar, un aprendizaje basado en problemas o por proyectos, nuevas formas de evaluación etc. La práctica docente consiste, además de enseñar conocimientos, en plantear o diseñar tares vinculadas a contextos de los alumnos, que supongan movilizar contenidos declarativos, procedimientos y actitudes. El enfoque por competencias altera determinados roles y tareas docentes, así como le otorga un papel más activo al alumnado. Así, pasar de la trasmisión y memorización del conocimiento al desarrollo de competencias, hace más enriquecedor el papel del profesorado. El docente desempeña más el rol de facilitador o mediador, guía o acompañante, para lo que debe ser capaz de diseñar “tareas” o situaciones de aprendizaje que posibiliten resolver problemas, aplicar los conocimientos y promover la actividad de los niños y niñas.

Existen infinidad de juegos para trabajar las matemáticas, mencionaremos algunos de ellos clasificándolos como hemos hecho anteriormente, según contenidos matemáticos.

Comenzaremos exponiendo un juego que abarca una serie de tareas que los niños deberán ir resolviendo una serie de tareas o problemas sencillos. En esta especie de juego los niños y niñas ponen en juego su competencia matemática de forma globalizada, activa y vivencial.

Resolución de problema. “Reparto del almuerzo especial”: se realiza una vez por semana en la clase de 5-6 años. Consiste en que el maquinista y su ayudante deben invitar al resto de compañeros a un almuerzo especial un día a la semana. Este juego pone en marcha la competencia matemática de los niños ya que deben resolver un problema fundamental: el reparto del almuerzo a través de una serie de estrategias:

1. El día anterior al almuerzo maquinista y ayudante se reúnen para acordar el tipo de alimento que quieren llevar a clase (en este caso, galletas de chocolate).
2. Tendrán en cuenta el número total de alumnos que son en clase para que nadie se quede sin almuerzo (20 alumnos/as)
3. Además, deberán decidir cuántas galletas quieren repartir a cada uno (en este caso acordaron traer 3 galletas para cada compañero/a).
4. Deberán considerar el almuerzo lo traerán a medias entre maquinista y ayudante por lo que surge la noción de división que los niños resolverán a través de dibujos y la representación visual de cantidades.

Todo un reto matemático que los niños y niñas irán perfeccionando a medida que practiquen, se equivoquen y acierten.

En resumen, en la siguiente situación o problema, maquinista y ayudante deben tener en cuenta que son 20 alumnos en clase, además han decidido que repartirán 3 galletas a cada alumno/a y que por lo tanto el total de galletas que deben traer son 60. Han llegado a la conclusión de que deben repartirse la tarea entre ambos, por lo que cada uno deberá traer desde su casa un total de 30 galletas para que cada compañero y compañera almuerce tres galletas de chocolate.

Para finalizar, maquinista y ayudante escriben una carta dirigida a los padres pidiendo ayuda y explicándoles el almuerzo que deben llevar a clase el día siguiente. En esta carta explican a través de la escritura y de imágenes en la cantidad de galletas que debe llevar cada uno. La maestra revisa si la operación está bien hecha pero nunca da la solución. Los alumnos y alumnas deben equivocarse para que mediante el ensayo-error encuentren la solución correcta. La maestra nunca dará la respuesta, y si existen dudas, realizará preguntas intentando orientar la respuesta del alumno o alumna o en su caso volverá a repetir la consigna de otra manera hasta que el alumno de con la respuesta.

Representación de la cantidad de galletas como herramienta de conteo de un niño de 6 años:

Las investigaciones sobre las estrategias de repartición en las primeras edades han puesto de manifiesto que los alumnos necesitan realizar dibujos y estos son utilizados como soportes visuales y como herramientas de conteo (Fuson y Li, 2009).

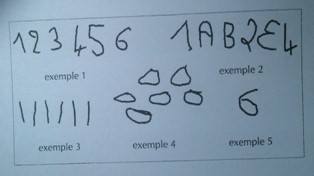
Formas de representación de cantidades de niños y niñas de 5 y 6 años como herramienta de conteo.

Momento en el que maquinista y ayudante agrupan sus galletas.

Además a la hora de repartir el almuerzo podemos trabajar la seriación con otro juego: El alumno elige de que forma va a repartir el almuerzo (por ejemplo: sentados en un corro el maquinista decide repartirle al primero pero al siguiente no, al siguiente si, al siguiente no, sí, no sí no, y así, succesivamente hasta que termina de repartir todas las galletas a todos los alumnos.

Despues del almuerzo todos los compañeros representan en un folio la serie que ha eleguido el maquinista para el reparto. Para representar mentalmente la serie y poder trasladar el pensamiento al folio, los niños y niñas asignan un símbolo para cada consigna  (si/no), de tal forma que se pueda representar en un dibujo la seriación elegida por el maquinista para el el reparto.

En la siguiente imagen observaremos que el maquinista eligue el simbolo B para representar “Sí” y el símbolo I para representar “no”. Éste es el resultado:

Representación a modo de seriación del momento del reparto.

Sumas y restas en el rincón de la peluquería: el rincón simbólico como el rincón de la peluquería o el supermercado (en la clase de 5 años) son contextos idoneos para jugar con las matemáticas y realizar sumas y restas de forma divertida. Los niños juegan a cortarse el pelo, a ponerse rulos, y deben de enfrentarse a problemas de la vida cotidiana donde se deben hacer cálculos para realizar pagos, devoluciones, etc.

Precios del rincón de la peluquería acordados por un grupo de alumnos y alumnas de tercer nivel del 2º ciclo de Educación Infantil.

También se pueden trabajar las sumas y las restas con el juego de los bolos. Cada alumno va a apuntando en la pizarra el número de bolos que ha tirado, al finalizar diez tiros se suma el total de bolos y se discute quien a tirado más y quien menos. Tambien se puede ampliar la actividad encontrando la diferencia entre ambos.

“Los bolos” para trabajar sumas y restas.

Noción de peso y descomposición numérica. El siguiente juego va acompañado de unas fichas que reparte la maestra y en las que indica los números que hay que descomponer, por ejemplo, el 9. La maestra coloca los nueve plátanos en una de las manos del mono de tal manera que se inclina rápidamente hacia ese lado. Los algunos investigan mediante ensayo error qué números sumados ambos dan un total de 9. Colocan plátanos en la otra mano del mono y la balanza se va equilibrando hasta que el niño/a comprende gracias al equilibrio de la balanza que ha resuelto el problema planteado.  En la ficha escribirá sus averiguaciones, por ejemplo: (4+5=9; 2+7=9; 1+8=9; 6+3=9, etc.)

Juego de mesa Monkey math: descomposición numérica y peso.

Conclusiones

A través de este artículo hemos visto que mediante las representaciones artísticas, los cuentos y las tareas o problemas que se esconden tras los juegos, puede trabajarse la competencia matemática en su totalidad, de manera real y de forma vivencial tanto los contenidos y objetivos que establece el currículum de 2ºciclo de Educación Infantil.

A través de su lectura podemos constatar que los aprendizajes matemáticos que se dan en  estos contextos y situaciones, al igual que las situacioens problema que prepara el maestro son los medios por los que los niños y niñas de hoy en día desarrollan la competencia maemática.

También se ha podido comprobar que se pueden crear contextos didácticos como el juego del reparto del almuerzo especial en los que el propio entorno proporciona la suficiente información al niño sobre su intento. Cuando los pequeños y pequeñas se dan cuenta de que los números (objetos) son además de palabras, cantidades, es entonces cuando el número (objeto hasta el momento)  adopta un valor de  herramienta, la cual servirá para resolver diferentes situaciones y problemas.

De esta manera también podemos afirmar que dichas propuestas pedagógicas (el juego, el cuento y el arte) incorporadas en las situaciones didácticas que organiza el maestro, ayudan además de a superar las limitaciones cognitivas que todos los niños tienen por su condición de niños (Egocentrismo, sincretismo, etc.) a desarrollar las capacidades innatas que todos los niños y niñas tienen.

La narración de cuentos en Educación Infantil, no solo ayuda en el área de lenguaje, sino que se vuelve una herramienta didáctica importante en el desarrollo de otras áreas como la lógica-matemática, fortaleciendo habilidades de está, relacionadas con los colores, tamaños, formas geométricas, el cálculo, las nociones espaciales, el conteo de objetos. Y que, por lo tanto, el cuento es un buen medio globalizador, a través del cual podemos motivar a los estudiantes en la asignatura de matemáticas.

Se puede cambiar esa actitud generalizada de rechazo ante las matemáticas desde edades tempranas, al no presentársele como un compendio de conceptos abstractos e incomprensibles para ellos/as..

La metodología de los rincones, el juego que se produce en ellos y el reparto que se hace del rincón pueden suponer contextos muy ricos de aprendizajes matemáticos.

Cuando un alumno realiza y evalúa una práctica matemática, como en el caso del almuerzo especial, activa un conglomerado formado por situaciones problema, representaciones, conceptos, proposiciones, procedimientos y argumentos, articulado en la configuración (Godino, Font y Gallardo, 2013).

En este artículo se ha presentado una secuencia de  propuestas y actividades de forma bastante descriptiva, ya que, entendemos que más que dar una secuencia cerrada de actividades a implementar, preferimos mostrar  una narración ordenada  de una posible   secuencia para que pueda  servir de referente a los maestros . Entendemos que, partiendo de estos recursos (juegos, obras de arte, y cuentos), cada docente debe rediseñar las actividades que favoreceran el desarrollo de la competencia matemática en su grupo de alumnos.