El método Singapur está considerado como un modelo muy prestigioso de la reflexión sobre la convivencia o no de implantarlo en nuestras aulas, en el sistema educativo español, en base al evidente paralelismo sobre la lamentable situación en la que se encuentran nuestros escolares en la actualidad en el ámbito de las matemáticas y aquella en la que encontraban nuestros escolares en la actualidad en el ámbito de las matemáticas y aquella en la se encontraban los alumnos de La República de Singapur al comienzo de la década de los 80, según diferentes pruebas comparativas internacionales como el informe PISA.
Incidiendo en lo anterior, extender esta reflexión sobre los problemas u obstáculos que conllevaría su implantación en las aulas españolas.
Palabras clave
Metodología Singapur; Resolución de problemas; Matemáticas; Visualización reflexiva; Currículo en espiral; Enfoque C-P-A; Variación sistemática; Modelo de barras.
The “Singapore Method” is considered a very prestigious model of mathematics teaching. The main purpose of this work is to contribute to the reflection on the coexistence or not of implanting it in our classrooms, in the Spanish educational system, based on the evident parallelism on the lamentable situation in which our students are currently in the field of mathematics and that in which students from the Republic of Singapore found at the beginning of the 80s, according to different international comparative tests such as the PISA report.
Influencing the above, extend this reflection on the problems or obstacles that would entail their implementation in Spanish classrooms.
Keywords
Methodology Singapore, problem resolution, mathematics, reflective visualization, curriculum in spiral, approach C-P-A, systematic variation, bar model.
1. Nacimiento del método Singapur (MS)
Con apenas el 1,5 % de superficie cultivable, importando de Malasia el agua potable de la que carecían, con una población de algo más de 5 millones, Singapur apostó por lo único que tenía: sus habitantes. En ello encontramos la explicación del objetivo sobre lo que gira la educación en este país: lograr que todos los niños desarrollen sus capacidades, despertando su interés durante toda su vida por aprender y descubriendo sus potencialidades.
1.1. Sus orígenes
Como hemos anticipado, el problema sobre el bajo nivel de los alumnos en las pruebas escolares internacionales hace que, a principios de los 80 el Ministerio de Educación de Singapur se propusiese idear un nuevo modelo de enseñanza matemático.
La editorial Mashall Cavendish Education en 1982 publicó los primeros materiales didácticos. Desde entonces hasta nuestros días estos materiales considerados muy exitosos han sido revisados, en base a las experiencias y reflexiones sobre la práctica docente. Comprenden desde la Educación Infantil hasta los últimos cursos de la Educación Secundaria.
A partir de 1995 los escolares singapurenses están logrando excelentes resultados en las pruebas externas.
1.2. Situación actual
El sistema educativo de Singapur ha sido declarado por los más relevantes expertos internacionales como uno de los mejores del mundo, en vista a las primeras posiciones (lideran la prueba PISA) y excelentes resultados que sus alumnos logran en las diferentes pruebas internacionales como TIMMS, PISA o PIRLS.
Los alumnos de Singapur cuentan con competencias muy valoradas como la innovación, la capacidad para conducir la incertidumbre y el afán por la experimentación en la búsqueda de soluciones matemáticas alternativas. Si las comparamos con las competencias matemáticas de nuestros alumnos en España seguramente, como mínimo, debería provocar inquietud e insatisfacción en el sector docente.
Todo ello ha motivado que el Método Singapur haya tenido una expansión mundial. En Singapur se utiliza este Método no sólo para la enseñanza de las Matemáticas, sino también de las Ciencias y del Lenguaje.
En cuanto al currículo se refiere, en Singapur se tratan menos temas pero con mayor profundidad. Está probada su efectividad en la resolución de problemas dando así instrumentos y habilidades que capaciten a los niños para los retos y el dinamismo de esta era. Aquí hallamos un nuevo punto para cuestionarnos la enseñanza matemática en nuestro país. ¿De qué sirven los amplísimos currículos del sistema educativo español? ¿Acaso esta amplitud no impide tanto a los alumnos como a los profesores el poderse detener a entender los temas?
La OCDE, en esta línea, se ha pronunciado recomendando reducir los currículos, reducir el número de temas pero tratarlos en más profundidad con actividades que cautiven el interés y la motivación de los estudiantes.
2. El método Singapur (MS)
2.1. Primera aproximación al modelo de enseñanza Singapur
El Método Singapur es conocido también como “Mastery Approach” (Enfoque de Maestría); “Maestría” no como procedimiento de “aprender para un examen” sino como búsqueda para la resolución de problemas.
Mahoney lo define como “una combinación entre el currículum, la pedagogía y la cultura”.
Para hablar con exactitud más que “Método” deberíamos decir “compendio metodológico” estructurado en torno a la resolución de problemas, mediante un aprendizaje activo en el que los alumnos estén interesados y vayan desarrollando sus capacidades intelectuales.
Está ideado basándose en los trabajos y postulados sobre el desarrollo y el aprendizaje de expertos internacionales como Jerome Brunes, Lev Vygotsky, Richard Skemp, Zoltan Deines…, incorporando los “principios fundamentales de aprendizaje” más adecuados en esta metodología. Ellos serían:
1. Visualización: de las matemáticas previo al aprendizaje abstracto.
2. Resolución de problemas: como eje vertebrador de la enseñanza de las matemáticas.
3. Matemática mental: en todos los niveles debemos incluir el cálculo mental aplicado a conocimientos matemáticos.
4. Dominio comprensivo: hay que comprender el problema para conseguir el dominio matemático a través de la praxis.
5. Estrategias: utilizar múltiples estrategias para resolver un problema implicará mayor habilidad matemática.
2.2. Características del Método Singapur y sus fundamentos teóricos
Insistiendo en que la Metodología Singapur surge de la combinación de los planteamientos sobre aprendizaje más exitosos de la segunda mitad del siglo XX para intentar lograr lo que todos los docentes se proponen a la hora de enseñar matemáticas: un aprendizaje donde aprehendan los fundamentos matemáticos, significativos y útiles para el alumno y que perduren y utilicen en toda su vida.
En este contexto de perdurabilidad, y en base a las ideas de fragmentación y las tres etapas de la memoria de Miller: memorización icónica (es sensorial y su duración es de unos segundos), memoria a corto plazo (operante y su duración es de 15-20 segundos) y memoria a largo plazo (de acumulación y su duración es de manera duradera); los alumnos del Método Singapur trasladan fácilmente sus prácticas sensoriales ubicadas en su memoria icónica a los ejercicios que utilizan la memoria a corto plazo. Desde la reiteración con distintos componentes (Variación Sistemática, Currículo en espiral que ahora veremos) transfieren a la memoria a largo plazo lo enseñado mediante asociaciones que crean competencias permanentes para el futuro adulto. Este método consigue que se acuerden de “el qué”, “el cómo” y “el para qué” de las ideas matemáticas.
La proposición del “Método Singapur” destaca que un correcto diseño de enseñanza debe relacionar los objetivos de la formación con los diversos ejercicios a realizar con los discentes. El prototipo de docencia de este método configura sus ejercicios según este gráfico.
Imagen 1. Modelo de enseñanza (fuente: Método Singapur)
Cuando administramos el modelo en nuestro proyecto de instrucción, cada sector de éste tiene sus objetivos propios y, como consecuencia, sus propios ejercicios.
Lev Vygotsky también deja su influencia en el “Método Singapur” al señalar el importante papel de las relaciones sociales en el aprendizaje infantil. Ello explica el trabajo cooperativo como componente de la enseñanza. Para el niño la práctica con iguales en el aprendizaje matemático ayuda a su entendimiento y/o lo refuerza. Otro propósito de Vygotsky es el de enseñar adaptando los contenidos a la “Zona de Desarrollo próximo”; estas zonas señalan “qué” debe conocer el alumno, y “cómo” debe conocerlo según su fase de crecimiento personal. En la imagen aparece el resumen de la “Zona de desarrollo próximo”.
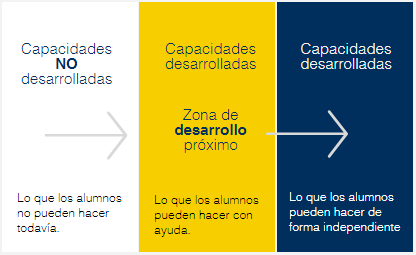
Imagen 2. Zona de desarrollo próxim (fuente: Método Singapur)
Bruner, por su parte, realiza una doble aportación al Método que se erigen como dos de las cuatro características fundamentales del MS, y que son las dos primeras que ahora desarrollamos: el Enfoque C-P-A y el Currículum en espiral.
a) El Enfoque C-P-A (Relacionado con las etapas de aprendizaje y los tipos de representación).
Según Jerome Bruner, la enseñanza es un procedimiento dinámico, y para conseguir una comprensión completa de los conceptos matemáticos es imprescindible una preparación en la que los alumnos deban atravesar 3 fases: ENACTIVA, ICÓNICA y ABSTRACTA. Cada una de ellas se caracteriza por un tipo de representación. De este modo nos encontramos con:
- Representación enactiva: el objeto se conoce mediante la interacción directa con él (Ej.: hacer nudos en cordones, cuerdas…).
- Representación icónica: el objeto es representado mediante una imagen (dibujar un nudo).
- Representación abstracta: se utilizan símbolos para representarlo (escribir “nudo”).
“PRIMERO MANIPULAR, LUEGO DIBUJAR Y DESPUÉS LOS SÍMBOLOS”.
Aplicándolo al Método Singapur:
El enfoque Metodológico es el llamado C-P-A correspondiente a cada una de las etapas de Bruner:
CONCRETO (Enactiva) – PICTÓRICO (Icónica) – SIMBÓLICO (Abstracta).
Durante la fase enactiva los niños se relacionan con elementos manipulativos concretos, utilizando un instrumental real, tangible, conocido y a su alcance para indagar en los conceptos matemáticos. En la segunda fase (Icónica) se les debe pedir que dibujen un modelo pictórico que representen las cantidades matemáticas y las correspondencias entre cuantías o los desarrollos matemáticos ocultos que hagan posible la solución del desafío o el problema que deben averiguar. En la tercera y última fase (Abstracta) cuando ya están familiarizados con los conceptos los niños estructuraran algoritmos usando símbolos y signos matemáticos para interpretar las experiencias “concreta” y “pictórica”.
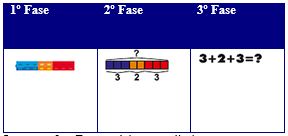
Imagen 3. Fases del entendimiento conceptual (fuente: Método Singapur)
b) Currículum en espiral.
En el MS el currículo está diseñado en forma de espiral. Los temas se trabajan de forma gradual, y cuando los escolares adquieren nuevos conocimientos refuerzan los anteriores. Esta planificación gradual posibilita la evaluación del aprendizaje por parte del profesor en todo momento (evaluación continua). Ocasiona un aprendizaje comprensivo y significativo, precisamente lo contrario a lo que ocurre en los currículos lineales como el nuestro, en los que encontramos un aprendizaje operacional.

Imagen 4. Currículum en espiral (fuente: Fundamentos teóricos del Método Singapur)
Bruner dice en “El proceso mental en el aprendizaje”: “Un plan de estudios ideal es aquel que ofrece materiales y contenidos de enseñanza a niveles cada vez más amplios y profundos y, al mismo tiempo, que se adapten a las posibilidades del alumno definidas por su desarrollo evolutivo. Por tanto, el currículum debe ser en espiral y no lineal, volviendo constantemente a retomar y a niveles cada vez más elevados los núcleos básicos o estructuras de cada materia. Estas estructuras o núcleos básicos tienen que ser convertidos a los tres modos fundamentales de representación según las posibilidades evolutivas del niño: enactiva (ejecutora o manipulativa, que corresponde al estadio sensoriomotor de Piaget), y que se refiere a aquello que se adquiere a través de la acción del organismo en el mundo; icónica (corresponde a la etapa preoperativa); y simbólica (etapa lógico concreta y lógico abstracta) según que lo predominante en su modo de asimilar la realidad sea la acción, la intuición o la conceptualización”.
c) Variación sistemática y perceptual.
Este concepto se basa en la teoría de Zoltan Deines quien enfatiza en la idea de evitar las repeticiones y en su lugar presentar el mismo sistema de tantas maneras perceptivas como sea factible. El planteamiento sería introducir modificaciones en un mismo procedimiento. Los conceptos matemáticos se les muestran a los escolares de forma sistemática mediante tareas variadas. Así, como sostiene Deines, las diferentes formas de ilustrar son muy importantes para el completo desarrollo de la comprensión relacional favoreciendo que los alumnos vayan consiguiendo la competencia matemática en cuanto a la abstracción nos referimos.

Imagen 5. Variabilidad Matemática: Triángulos (fuente: Método Singapur)
d) Resolución de problemas y el modelo de barras.
El Método Singapur concibe las matemáticas como medio para resolver problemas entendiendo el razonamiento lógico que subyace y además con un enfoque muy visual (dibujos, diagramas…) y a veces también auditivo. Los problemas que se trabajan en este Método motivan a los alumnos a plantearse nuevas incógnitas y a contrastar sus hipótesis. Tienen la misma importancia el resultado, el proceso que ha conducido al mismo y la explicación que de todo ello puede hacer el niño. Siempre hay más de una forma correcta de llegar a la solución de un problema.
En ello inciden los siguientes aspectos: Actitudes, Metacognición, Procesos Habilidades y Conceptos. En el gráfico aparecen especificados los elementos que componen cada una de estas cinco dimensiones.
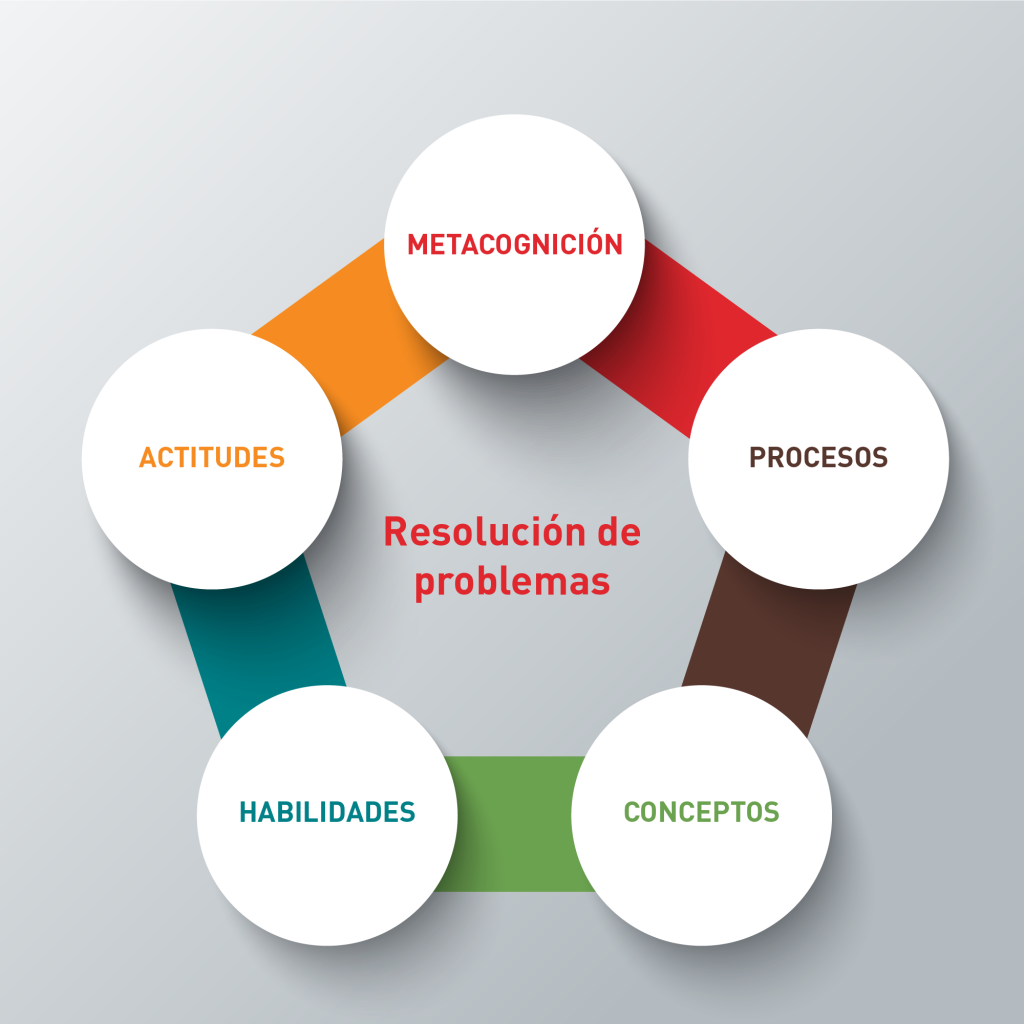
Imagen 6. Pilares básico para la resolución de problema (fuente: Polygon Education)
Precisamente para trabajar en los escolares la metacognición, en vez de incurrir de forma repetitiva en la memorización y utilización de fórmulas matemáticas (como ocurre como tónica general en el sistema educativo español), el MS utiliza un “paradigma de comprensión conceptual”: el “Modelado de Barras”. Esta estrategia, distintiva del Método se vale de recursos visuales para que el pensamiento se haga visible.
Los niños así toman conciencia del “cómo aprenden”, poseen más autonomía para autorregular su aprendizaje (en especial niños con dificultades) al rectificar su pensamiento o reproducirlo adaptándolo a otros contextos.

Imagen 7. Modelo de barras (fuente: Blog Matemáticas maravillosas)
Íntimamente enlazado aparecen otras dos características básicas del Método: el papel del profesor ayudando y/o interviniendo en el proceso y la evaluación continua como retroalimentación del aprendizaje.
Existen diferentes tipos de modelados de barras. Todos, eso sí, participan en algo en común: promover el razonamiento lateral y creativo.
Hay además otras herramientas para el desarrollo de habilidades metacognitivas en los escolares, como por ejemplo realizar un “Diario Matemático”, “Cadenas Lógicas”, “Cubos Conectables”, “Rectas Numéricas”, etcétera.
3. El maestro como agente de cambio. Panorama actual en la enseñanza de las matemáticas en España: obstáculos y errores
El planteamiento Singapur necesita profesores que sean capaces de dar un giro extraordinario en su labor docente, precisa una gran formación para adaptar sus conocimientos al nuevo sistema, abandonar las clases magistrales para pasar, como hemos venido diciendo, a trabajar con los escolares de manera manipulativa y cooperativa. El MS abandera un aprendizaje activo de las Matemáticas y para ello los docentes necesitan sobreponerse a sus propios miedos o recelos a no comprender cómo piensan los alumnos. Cuando el maestro plantea un problema y en lugar de explicar cómo se resuelve, deja que sean los niños los que busquen la solución, generalmente aparecen resultados y procedimientos diferentes que retarán a los docentes a analizar y socializar lo que hicieron los propios escolares, tratando de pasar de la aplicación mecánica de un algoritmo a la representación algebraica.
En el MS, si los docentes se centran en el procedimiento, los alumnos tendrán pocos logros. Pasaría lo mismo si sólo se fijan en el cálculo o si provocan que el aprendizaje se haga de forma individual. Por el contrario, lo que se pretende es valorar las ideas e iniciativas de los alumnos e involucrarlos en definitiva en las primeras etapas del aprendizaje.
Frente a esto nos encontramos con obstáculos didácticos en la práctica, a veces por la dinámica e inercia de la tradición que hace que los docentes repitamos indefinidamente lo que aprendimos de nuestros profesores en el pasado.
El rol docente, no sólo para llevar a cabo el Método Singapur en su aula sino para que realmente se erigiera como auténtico motor de cambio hacia un nuevo modelo de enseñanza, requiere someterse a una profunda reflexión sobre qué, para qué y cómo se enseñan las matemáticas.
Conclusiones
Parece obvia y probada la efectividad del Método Singapur antes los logros conquistados en la población en este país.
La incorporación a la enseñanza de algunos elementos de MS por más de 50 países (EEUU, Inglaterra, Islandia…) muestra el interés que despierta. Su expansión y popularidad está justificada por los excelentes resultados obtenidos. Conviene recordar, sin embargo, las dificultades encontradas en su aplicación cuando se ha implantado a partir de los 10 años. Si aseguramos que este método hace que los alumnos lleguen a entender las matemáticas de manera significativa e individual, es decir, que cada niño avanza y progresa a su ritmo, pudiéndole dar un sentido y resolución a los problemas de la vida cotidiana y contribuyendo a la adquisición de la competencia matemática parece evidente que es en la Educación Infantil y Primaria donde sería más conveniente su implantación dada la concordancia entre los “principios fundamentales” de esta metodología y las edades de los infantes en estas etapas de la enseñanza, abandonando el clásico esquema actual “memorización-repetición”. Si a todo ello sumamos, la motivación que supone para el alumno este modo de adquirir contenidos matemáticos, con seguridad estaremos incidiendo en uno de los hándicaps de la educación en España: la falta de interés en el aprendizaje matemático.
Sería justo ampliar mucho más nuestra reflexión hacia algo de absoluta trascendencia y de vital importancia para la puesta en práctica de este Método: el importantísimo papel que debe jugar el profesor. Su convencimiento primero y después formación sobre esta nueva metodología, junto a la descarga de contenidos curriculares en matemáticas implicaría nuevamente contar con medidas gubernativas para favorecer un necesario y urgente cambio de rumbo en la enseñanza de esta materia.
Referencias
- Alonso, C., López, P. y De la Cruz, O. (2013). Creer Tocando. Tendencias Pedagógicas, 21, 249-262.
- Alvarez Marañón, G. (2012): El arte de presentar. Barcelona: Gestión 2000.
- Ban Har, Y. (2012): Seminario de Matemáticas Singapur en Chile. Universidad de Santiago de Chile: Marshall Cavendish Institute.
- Barría, C. (2018): Cómo es el “Método Singapur” con el que Jeff Bezos les ha enseñado matemáticas a sus hijos (y por qué lo usan los mejores estudiantes del mundo). Consultado 16-07-2018 en https://www.bbc.com/mundo/noticias-42966905
- bruner, J. (2001): El proceso mental en el aprendizaje. Madrid: Narcea.
- Cosme, A. (2018): Tips para el uso de Materiales Manipulativo en Resolución de Problemas con Método Singapur. Edelvives.
- Escobar, C. (2018): Método Singapur – Modelos Suma, Resta, Multiplicación y División para Segundo Básico. Consultado 01-08-2018 en http://matematicas-maravillosas.blogspot.com/2012/05/metodo-singapur-modelos-suma-resta.html
- Eres mamá (2017): ¿Qué es el Método Singapur para aprender matemáticas? Consultado 30-07-2018 en https://eresmama.com/que-es-el-metodo-singapur-para-aprender/
- Inostroza, F. (2014): Fundamentos Teóricos del Método Singapur. Consultado 01-08-2018 en https://es.slideshare.net/profedoc/fundamentos-tericos-del-mtodo-singapur-cvd
- Kheong, F. H.; Ramarkrishnan, C.; Choo, M. (2012): Pensar sin límites. Cuaderno de Trabajo para el estudiante 1A. Marshall Cavendish Education.
- Kheong, F. H.; Ramarkrishnan, C.; Choo, M. (2012): Pensar sin límites. Cuaderno de Trabajo para el estudiante 3A. Marshall Cavendish Education.
- Larrocha, J.; Álvarez, G; Moscoso, A.; González, F. y Leo, J. M. (2011): La teoría de J. Bruner sobre el desarrollo cognitivo. Consultado 16-07-2018 en http://psicodesarollo1b.blogspot.com/2011/05/la-teoria-de-jbruner-sobre-el.html
- Método Singapur (2013): Método Singapur. Nuevas Matemáticas para profesores innovadores. Consultado 04-07-2018 en https://www.metodosingapur.com/
- Polygon Education (2016): ¿Por qué Matemáticas Método Singapur? Consultado 03-07-2018 en http://www.polygoneducation.com/productos/pensar-sin-limites-matematicas-metodo-singapur/
- Rodríguez, S.V. (2011). El método de enseñanza de matemática Singapur: “Pensar sin límites”. Revista Pandora Brasil, 27, 1-3.

